Acides et bases

b) CH3COOH + H2O = H3O+ + CH3COO -
La réaction tend vers un équilibre: on peut appliquer la loi d'action des masses:
Ka = 10-5


















Définitions des acides et des bases
Il existe plusieurs définitions des acides et des bases. Elles sont toutes valables dans certains domaines.


Selon Arrhenius ( vers 1890 )
•
•
•
•
•
•

un acide est un corps capable de donner un proton ( ion H+ ).
une base est un corps capable de donner un ion OH- en solution aqueuse (dans l’eau ).
Selon Brønsted ( 1923 )
un acide est un corps capable de donner un proton H+ à une base.
une base est un corps capable d'accepter un proton H+ d'un acide.
Selon Lewis ( 1923 )
un acide est un corps capable d’accepter une paire d’électrons.
une base est un corps capable de donner une paire d’électrons.
Petit rappel
L’électron est une particule chargée négativement. On peut le noter e -
Si un atome gagne un électron: il devient un ion négatif (= une particule chargée négativement )
Exemple: l’atome de fluor gagne un électron et devient un anion (= ion négatif )
F + e- = F-

Si un atome perd un électron: il devient un ion positif (= une particule chargée positivement )
Exemple: l’atome d’aluminium perd 3 électrons et devient un cation ( = ion positif )
Al = Al3+ + 3 e-
L’atome d’hydrogène (symbole chimique: H) est le plus simple de tous. Il est formé d’un noyau formé d’une seule particule: un proton, chargé positivement (+) et d’un seul électron “satellite” chargé négativement ( - ).
On peut représenter simplement un atome d’hydrogène:
Si un atome d’hydrogène perd son électron ou se le fait “voler”, il ne reste qu’un proton.
On peut donc noter :

Retour aux acides
Reprenons la définition de Brønsted ( 1923 ) :
•
•
un acide est un corps capable de donner un proton H+ à une base.
une base est un corps capable d'accepter un proton H+ d'un acide.
Cette définition nous montre qu'à tout acide, correspond une base, et réciproquement.
Exemple: acide base proton

On dit que l'acide et la base forment un couple acide - base , et on le note :


Produit ionique de l’eau
Considérons la dissociation électrolytique de l'eau pure ( autoprotolyse de l'eau )
Appliquons la loi d'action de masse :
Ou :
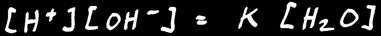
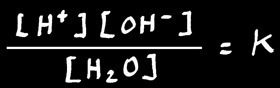

Dans ce cas, K est très petit: la dissociation de l'eau est très faible; on peut donc considérer la concentration de l'eau dans l'eau comme une constante valant :

Le produit de 2 constantes étant égal à une constante, nous pouvons définir le produit ionique de l'eau :
Retenons qu'à une température ordinaire de 25 °C :


Avec :
Caractère amphotère de l’eau

L'eau est amphotère. Elle peut soit donner , soit recevoir un proton .
Caractère acide de l'eau :
Caractère basique de l'eau :
H2O + H+ = H3O+
H2O = H+ + OH-

Réaction de protolyse
La protolyse est l'échange de proton entre acide (donneur) et base (accepteur). Prenons l'exemple de 2 couples acide-base, soit :
et
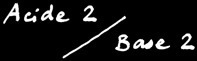

Alors on peut écrire l'équation de la protolyse :

Si on applique la loi d'action de masse , on trouve :
Si K est grand, l'équilibre est fortement déplacé vers la droite, autrement dit, l'acide 1 est plus fort que l'acide 2.

Plus un acide est fort (plus il a tendance à donner un proton H+), plus sa base conjuguée est faible (moins elle a tendance à accepter un proton H+). Evidemment, la réciproque est également est vraie. Le Ka de l'acide sera une mesure de la force de l'acide, et par conséquent, de la base conjuguée .
acide fort
base très faible
a)

L'équilibre est fortement déplacé vers la droite: Ka = 109
acide faible
base faible

La réaction est fortement déplacée vers la gauche: Ka = 10-23
c) NH3 + H2O = H3O+ + NH2-
base forte
acide très faible
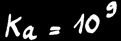
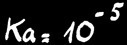

Dans ce cas NH3 a plutôt tendance à accepter un proton H+, réagissant comme une base.
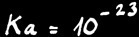
Nous allons étudier les acides forts , les bases fortes , dont l'équilibre de protolyse est totalement déplacé, ainsi que les acides et bases faibles qui mènent à un équilibre dont il faudra tenir compte.
Exemple : mettons de l'acide chlorhydrique dans l'eau. La réaction de protolyse s'écrit:
acide 2

acide 1
base 1
base 2
L’eau est un acide très faible: elle a donc tendance à accepter le proton H+ cédé par l’acide fort HCl, et jouer ainsi le rôle de base. Dans ce cas la protolyse est totale: K est grand et on écrit:
Remarque :

Le cation H3O+ correspond à un ion H+ associé à une molécule d'eau. Nous utilisons indifféremment ces deux expressions.
Par exemple, nous aurions aussi pu écrire l'équation de l'autoprotolyse de l'eau:
Nous aurions abouti au produit ionique de l'eau:

Acidité et basicité d’une solution aqueuse
Définitions :

Une solution aqueuse est dite
acide si
neutre si
basique si

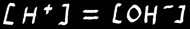

Conséquence :
Dans une solution neutre :
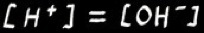
Or ,
Dans une solution acide :
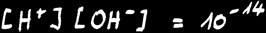
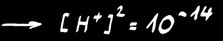
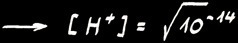
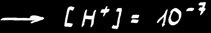
Dans une solution basique :




Solutions aqueuses diluées d’acides forts
Seules les solutions diluées seront abordées dans ce cours. Lorsqu'on s'intéresse à des solutions concentrées, l'interaction entre les ions en présence compliquent le problème .
Les acides forts sont les acides dont l'équilibre de protolyse est totalement déplacé vers la droite: ils sont totalement dissociés .
Exemples :

Si l'on affaire à de tels acides, on symbolise la réaction par une simple flèche, et on écrit:

Avec [ H3O+ ] = [ HNO3 ] introduit
Dans ces problèmes, on considère [ H3O+ ] issue de l'autoprotolyse de l'eau comme négligeable en comparaison de la [ H3O+ ] introduite sous forme d'acide fort.
Dans une solution aqueuse diluée, [ H2O ] est toujours constante:
On peut donc écrire ( à 25°C ) : [ H3O+ ] [ OH- ] = Ki = 10 -14

Quelles sont les concentrations [ ] de H3O+ et OH- d'une solution de 2L d'acide nitrique, si l'on introduit 6,3 mg de HNO3 ?
Réponse : HNO3 est un acide fort: sa protolyse est totale.
On écrit : HNO3 + H2O = H3O+ + NO3-

[ H3O+ ] = [ HNO3] introduit
[ H3O+ ] = (6,3 x 10-3) / (2 x 63) = 5 x 10 -5 M
[ OH- ] = Ke / [ H3O+ ] = 10-14 / (5 x 10-5) = 2 x 10 -10


Solutions aqueuses diluées de bases fortes

Dans le cadre de ce cours, on ne considérera que la base forte OH -. Sa réaction de protolyse avec l'eau:
H2O + OH - = OH - + H2O
Montre que [ OH - ] en solution = [ OH- ] introduite.
Remarque :
Les OH - sont introduits en solution sous la forme d'un oxyde ou d'un hydroxyde, dont il faudrait, en toute rigueur connaître la solubilité et le degré de dissociation. On simplifie le problème en n'utilisant que des hydroxydes et oxydes de métaux alcalins et alcalino-terreux que l'on considère comme totalement dissous ou dissociés .
Exemple :
On en conclut que : [ OH - ] = [ NaOH ] = 2 [ Na2O ]


Trouver les concentrations de toutes les espèces chimiques en solution, sachant que l'on introduit 200 mg de NaOH dans 2,5L d'eau .

Réponse :
NaOH est un hydroxyde de métal alcalin. Il est donc totalement dissocié selon:

[ Na + ] = [ NaOH ] = ( g/L ) / (NaOH) = (2 x 10-1) / (2,5 x 40) = 2 . 10 -3 M
[ OH - ] = [ NaOH ] = [ Na + ] = 2 . 10 -3 M
[ H2O] = constante = 55,5 M
[ H3O+] = Ke / [ OH - ] = 10 -14 / (2 x 10 -3) = 5 . 10 -12 M


Quelle est la concentration en H3O+ d'une solution aqueuse, sachant qu'on a mis 1g d'oxyde de magnésium dans 1m3 d'eau ?

Réponse :
[ OH- ] = 2 [ MgO ] = (2 x 10 -3) / (MgO) = (2 x 10 -3) / 40 = 5 . 10 -5 M
[ H3O+ ] = Ke / OH- = 10 -14 / (5 x 10 -5) = 2 . 10 -10 M
Solutions aqueuses diluées d’acides faibles
Les acides faibles sont ceux dont l'équilibre de protolyse est plutôt déplacé vers la gauche: leur dissociation n'est pas totale .
Exemples : CH3COOH , H2CO3 , HCN , HF , NH4 +, …
Etudions le cas d'une solution d'acide acétique CH3COOH
Dans ce cas, ainsi que dans le cas de tous les autres acides faibles, la concentration des ions H3O+ n'est pas si aisée à connaître que dans le cas des acides forts .

En effet, il faut tenir compte du Ka de l'acide. Appliquons la loi d'action des masses à cet équilibre :
( [ H3O + ] [ CH3COO - ] ) / ( [ CH3COOH ] [ H2O ] ) = K
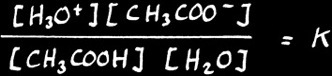
Comme nous l'avons déjà vu, [ H2O ] exprime la concentration de l'eau dans une solution aqueuse diluée: c'est une constante. On peut donc écrire :
( [ H3O+ ] [ CH3COO - ] ) / [ CH3COO -] = Ka
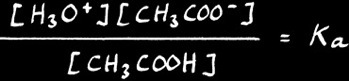
Ka est la constante acide .
Dans le cas de CH3COOH , Ka = 1,8 . 10 -5
Table des valeurs de Ka

Solutions aqueuses diluées de bases faibles
De même que les acides faibles, les bases faibles ont un équilibre de protolyse déplacé vers la gauche.
Exemples : CH3COO - , HCO3 - , CN - , F - , NH3
On remarque que les bases faibles sont les bases conjuguées des acides faible vu précédemment.
Etudions le cas de l'acétate CH3COO -
Alors ( [ CH3COOH ] [ OH - ] ) / ( [ H2O ] [ CH3COO - ] ) = K
Donc ( [ CH3COOH ] [ OH - ] ) / [ CH3COO -] = Kb

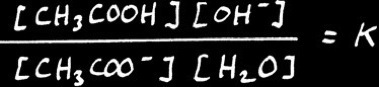
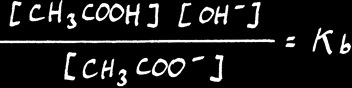

Remarques :
Pour éviter l'utilisation de Kb , il est bon de se souvenir que :
Ka . Kb = Ke et pKa + pKb = pKe
Le cas de CH3COOH : Ka = ( [H3O+] [CH3COO -] ) / [CH3COOH]
Le cas de CH3COO - : Kb = ( [OH -] [CH3COOH] ) / [CH3COO -]
Ka x Kb = ( [H3O+] [OH -] [CH3COOH] [CH3COO -]) / ( [CH3COOH] [CH3COO -] )
= [H3O+][OH-] = Ke
On utilisera donc dans le cas des acides comme des bases faibles le Ka de l'acide .
Dans ce but, nous avons reporté dans un tableau (à la page suivante), les valeurs des Ka et pKa se rapportant à différents couples acide-base. Dans tous les exercices relatifs aux acides et bases faibles, nous nous rapporterons à ces valeurs .
Les bases faibles sont introduites en solution sous forme de sel (en général alcalins) de l'acide conjugué .
Ex : CH3COO - peut être introduit sous forme de CH3COONa qui se dissocie dans l'eau en faisant apparaître les ions Na+ et CH3COO - .
Table des valeurs des Ka et pKa de quelques couples acide-base .
Remarques :
Les acides sont rangés dans ce tableau dans l'ordre de leur acidité décroissante, et par conséquent, leur base conjuguée devient de plus en plus forte à mesure que l'on descend dans le tableau .
On remarque que la somme des pKa de H3O+ et H2O = pKe
(Par exemple : -1,74 + 15,74 = 14)
Notion de pH
L'expression des concentrations en H3O+ et OH - des solutions aqueuses acides ou basiques est mal aisée: l'importante dilution de ces solutions fait que ces concentrations sont des nombres très petits. Dans le but de simplifier ces expressions, le suédois Sorensen a introduit la notion de pH qui se définit ainsi .
pH = -log [H3O+]
On peut aussi définir un pOH = -log [OH -]
Rappel concernant les logarithmes :
Quel est le pH d'une solution dont :
a) [H3O+] = 10 -4
b) [H3O+] = 2 x 10 -5
c) [OH -] = 5 x 10 -5
Si l'on se rapporte à la définition d'un eau acide , neutre et basique , que nous avons vu précédemment, on peut écrire :
Une eau acide a un pH < 7
Une eau neutre a un pH = 7
Une eau basique a un pH > 7
Il faut noter que l'échelle des pH est définie entre 0 et 14 , puisque nous avons déjà remarqué que :
[H3O+] [OH -] = 10 -14
ou pH + pOH = 14

pH des solutions aqueuses d’acides forts
Pour ces acides, [H3O+] est égale à la concentration d'acide introduit en solution. On trouve donc facilement le pH .
Calculer le pH d'une solution d'acide nitrique 10 -7 M .

Réponse :
pH des solutions aqueuses de bases fortes
Il est tout aussi facile de connaître [OH -] libérée par l'hydroxyde ou l'oxyde. On en déduit le pH au moyen du produit ionique de l'eau .
Trouver le pH d'une solution obtenue en dissolvant 4 mg de NaOH dans 10 L d'eau .

Réponse :
NaOH libère en solution aqueuse la base forte OH - .
[OH -] = [NaOH] = (4 x 10 -4) / 40 = 1 x 10-5
[H3O+] = Ke / 10 -5 = 10-9
pH = -log 10 -9 = 9
pH des solutions aqueuses diluées d’acides faibles
Ce problème est moins simple et nécessite la connaissance des constantes Ka (ou des pKa = -log Ka) de dissociation des acides. Il faut retenir la formule générale qui permet, à partir de la concentration [ ] de l'acide et de son Ka, de calculer son pH.
pH = 1/2 pKa - 1/2 log [ acide ]
Annexe: Pour ceux qui s'intéressent à l'établissement de cette formule, voici le cheminement qui permet, à partir de l'équilibre de dissociation de l'acide acétique, par exemple, d'y parvenir :
CH3COOH + H20 <--> CH3COO - + H3O+
( [CH3COO -] [H3O+] ) / [CH3COOH] = Ka
Ka [CH3COOH] = [CH3COO-] [H3O+] = [H3O+] 2
[H3O+] = √ Ka [CH3COOH] = ( Ka [CH3COOH]) 1/2
pH = -log ( Ka [CH3COOH] ) 1/2 = 1/2 ( -log Ka - log [CH3COOH] )
pH = 0,5 (pKa - log [CH3COOH])
Exemple: Calculer le pH d'une solution 10 -2 M d'acide acétique .
acide acétique CH3COOH = acide faible
de la table des Ka , on tire : Ka = 1,75 . 10 -5
--> pKa = -log Ka = 5 - log 1,75= 4,76
--> pH = 0,5 pKa - 0,5 log [CH3COOH] = 0,5 ( pKa - log [CH3COOH] )
= 0,5 (4,76 -log 10 -2)
= 0,5 (4,76 + 2) = 3,38
pH des solutions aqueuses diluées de bases faibles
On les introduit en solution sous forme de sel, dont il faudrait connaître la solubilité. Dans ce cours, nous n'aurons affaire qu'à des sels solubles et totalement dissociés.
Comme nous l'avons déjà vu, nous aboutissons à la définition d'un Kb, rattaché au Ka de l'acide conjugué, par la relation:
Ka . Kb = Ke
On traite le problème de la même manière que pour les acides faibles et on tombe sur la formule suivante:
pH = 7 + 1/2 ( pKa + log [ base ])
Exemple: Calculer le pH d'une solution de CH3COONa 10 -2 M. On considère l'acétate de sodium comme totalement dissocié:
CH3COONa --> CH3COO - + Na+
[CH3COO -] = [CH3COONa] introduit = 10 -2 M
avec pKs = 4,76
pH = 7 + 1/2 ( 4,76 + log 10 -2 ) = 7 + 0,5 ( 4,76 -2) = 7 + 0,5 (2,76)
pH = 8,4
1 .
2 .
3 .
4 .
5 .
6.

On introduit de l'oxyde de sodium dans 1 litre d'eau et on remarque que le pH a passé de 7 à 13,5 . Que s'est-il passé ? Combien de mg d'oxyde a t-il été introduit ?
Calculer le pH des solutions suivantes :
HNO3 0,1 M
NaOH 10 -2 M
HCl 0,5 mole/L
HClO4 2 . 10 -4 M
Quel est le pH d'une solution aqueuse contenant 1 gramme d'hydroxyde de sodium par litre ?
On met 5 g d'acide iodhydrique dans 10 litres d'eau . Calculer le pH .
Combien faut-il mettre de grammes de HCl dans 1L d'eau pour qu'il ait un pH égal à 3,5 ?
Nous voulons neutraliser 1 litre d'une solution aqueuse de NaOH 0,1 M . Quelle masse d'acide faudrait-il introduire si cet acide est : HCl ? H2SO4 ?

Retour au portail des sciences



Retour au portail de chimie



Suite du cours: les solutions




Suite du cours: l’électronégativité


Force d’un acide

Table des valeurs de Kb
1)
2)
3)
4)
logA (x . x' ) = logA x + logA x'
logA xB = B logA x
logA A = 1
logA 1 = 0
Une substance est amphotère si elle a un caractère à la fois acide et basique.
Définition:
Mesure simple du pH


Expérience
Le chou rouge, indicateur acide-base

Expérience


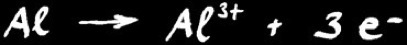

HNO3 est un acide fort , dont la protolyse est totale .
[H3O+] = [HNO3 -] = 10 -2
pH = -log 10 -2 = 2





Fin de la page
