Thermodynamique








1 cal = 4,19 J et 1J = 1N . 1m
La physique du XVIIIe siècle, autour de la mécanique newtonienne, décrit le monde comme un ensemble d'objets placés dans un espace à 3 dimensions (x, y, z). Chacun de ces objets peut être défini par sa position et sa vitesse.
La découverte de la gravitation explique la nature des forces dynamiques: la trajectoire est:
• légale (soumise à des lois naturelles)
• déterminée (de l'état initial du système on peut déduire tous les états suivants)
• réversible (théoriquement, on pourrait passer le "film" à l'envers).
Tous les phénomènes sont des apparences derrières lesquelles une grandeur ne varie pas: l'énergie.
L'énergie mécanique (Em) est la somme de 2 termes: l'énergie cinétique (Ec) et l'énergie potentielle (Ep).
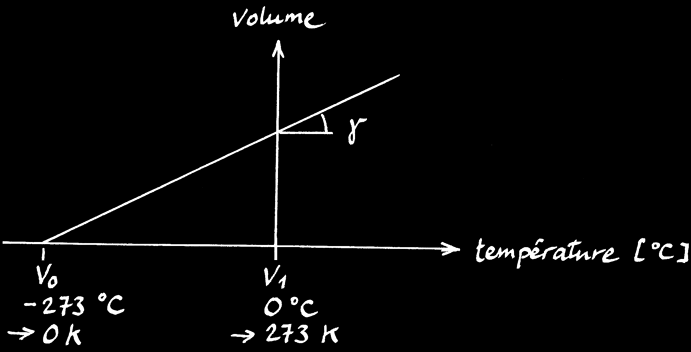
avec γ plus grand que dans les solides
Exemple: le thermomètre à mercure (Hg)

Historique

Chaleur et température





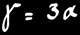

Or ce phénomène, interprété comme la diffusion dans la barre d'un fluide immatériel ( le calorique ) est:
• aussi naturel que la gravitation.
• descriptible mathématiquement.
• irréductible aux interactions dynamiques.
On a donc affaire à 2 universels antagonistes qui coexistent:
Dans un solide, les particules (atomes, molécules) oscillent autour d'une position d'équilibre. Plus on fournit d'énergie calorifique (chaleur) à ce corps, plus les particules s'éloignent de cette position d'équilibre. Le solide se dilate.
La chaleur (Q) reçue par un corps est l'énergie mécanique désordonnée reçue par ses particules. On écrit:
∆Q > 0 si l'énergie entre dans le système.
∆Q < 0 si l'énergie sort du système.
La température (T) d'un corps est la manifestation macroscopique de l'agitation des particules qui le composent. La température est égale à l'énergie cinétique (Ec) moyenne des particules d'un corps.
A une température donnée γ est le même pour tous les gaz.
1 calorie = 4,19 Joules
On écrit:
Exemple:
∆Q = c . m ∆T

Avec :
L'eau a une grande inertie thermique. Sa chaleur massique c=4200 J/Kg.K (10 fois plus que le cuivre ou le fer). Ça explique le rôle de modérateur climatique des plans d'eau (lac, mer, océan): l'eau absorbe beaucoup de chaleur quand il fait chaud et la restitue quand il fait froid.
Dans un corps hétérogène constitué de n parties ayant des chaleurs massiques différentes:
∆Q=(∑cimi)∆T = C∆T
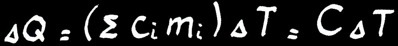
Applications: bilame (thermostat), jeu entre rails, joint de dilatation des ponts, fils électriques tendus,...
L'énergie calorifique est une quantité de chaleur. C'est une grandeur extensive (liée à la taille du système).
La température est une intensité de chaleur. C'est une grandeur intensive (non liée à la taille du système).
Pour Black (vers 1760):
•
•

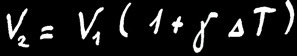
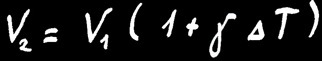
P
V
n
R
T
Avec :
Pression
Volume
nombre de moles
Constante des gaz parfaits
Température
•
•
La contradiction dure jusqu'au milieu du XIXe siècle. Joule décrit en 1847 l'énergie comme une réalité sous-jacente (sorte d'hypostase) à tous les phénomènes (électriques, chimiques, biologiques, mécaniques, lumineux, thermiques) qui se maintient à travers les transformations.
La thermodynamique est une science qui s'est développée au contact de l'industrie du charbon et des machines à vapeur. Elle est une réponse posée par la recherche du meilleur rendement de ces machines.
La thermodynamique introduit la notion d'irréversibilité chimique ( "l’allumette ne brûle qu'une fois" ... c’est aussi valable pour le pétrole et le charbon ! ) .
La gravitation, qui agit sur une masse inerte qui la subit dans son mouvement mais pas dans son essence.
La chaleur, qui transforme la matière (changement d'état), modifie ses propriétés intrinsèques.
Le monde ainsi décrit par la mécanique classique est idéalisé (les frottements associés aux mouvements ne sont pas pris en compte -> machines simples: poulies, treuils, leviers,...).
Le monde newtonien n'a pas d'évolution: des lois éternelles ordonnent le monde et l'esprit humain peut tenter de décripter au moyen des mathématiques le sens de l'oeuvre du Dieu créateur.
C'est une vision du monde déterministe: un être capable à un instant donné de connaître la position et la vitesse de toutes les particules de l'univers pourrait en déduire le passé comme l'avenir. Cette version sera combatue par Diderot, les Romantiques ainsi que de nombreux chimistes et médecins (Mayer).
En 1822, Fourier, dans sa "Théorie analytique de la chaleur" , étudie la propagation de la chaleur dans une barre:
"la chaleur se transmet perpendiculairement aux surfaces de même température, dans le sens des températures décroissantes et proportionnellement au gradient de température."
On note : Em = Ec + Ep
quantité de chaleur
chaleur massique (coefficient de proportionnalité qui dépend du corps étudié)
masse
différence de température
∆Q
c
m
∆T
Avec :
quantité de chaleur
capacité thermique
masse
différence de température
∆Q
C
m
∆T
Avec :
Différence de volume (accroissement ou diminution)
Volume initial
Volume final
coefficient de dilatation volumique , avec
différence de température
∆V
V1
V2
γ
∆T
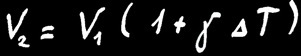

Joint de dilatation sur l’autoroute A9, viaduc de Chillon



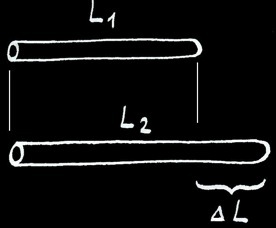
Si nous chauffons une barre de longueur L1, elle va se dilater et mesurera finalement la longueur L2.
L’allongement (∆L) va dépendre de la différence de température de la barre (∆T) et de la matière qui constitue la barre.
On note :
ou :


Nous pouvons facilement mettre en évidence la dilatation d’un métal sous l’effet de la chaleur et sa contraction lors du refroidissement.
Expérience:
corps chaud dilaté
corps froid contracté
Les atomes oscillent autour de leur position d’équilibre et prennent plus de place: le volume entier se dilate.
Les atomes gardent leur position: ils sont figés et occupent peu de place.
Prenons un solide avec des atomes bien rangés:
un cristal ou un métal par exemple.
Représentons chaque atome par un point:




∆L
L1
L2
α
∆T
Différence de longueur (allongement ou raccourcissement)
Longueur initiale
Longueur finale
coefficient de dilatation linéique ou linéaire
différence de température
Avec :
Dilatation linéique (= dilatation d’une barre)
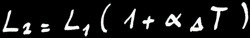

Dans la construction, il faut tenir compte de la dilatation des matériaux: les ponts, les bâtiments se dilatent et se contractent en fonction de la température ambiante: il faut donc prévoir un certain “jeu”, un joint de dilatation, pour que ces constructions ne craquent pas.
On appelle coefficient de dilatation linéaire ( α ) d'un corps solide, l'allongement que subit l'unité de longueur (1m) de ce corps lorsque sa température s'élève de 1°C. Plus le coefficient d’une matière est élevé et plus cette matière se dilate sous l’effet de la chaleur.
Exemple:
Une bilame se tord dans une flamme ... Pourquoi??
Expérience:


Le coefficient linéaire de l'acier est de 0,00001, ce qui signifie qu'une tige d'acier d'un mètre s'allonge de 0,00001m (ou 0,01 mm) pour une élévation de température de 1°C.





Cette notion entre en résonance avec d'autre champs de la pensée à l'époque de cette révolution industrielle:
•
•
La science historique fait son apparition et découvre un "sens de l'Histoire".
La biologie découvre l'évolution des espèces, le transformisme de Darwin.


La même quantité d'énergie (chaleur) provoque une grande augmentation de température dans un système ayant peu de particules et une petite augmentation de température dans un système ayant beaucoup de particules.
une tasse de café bouillant a une température plus élevée que celle du lac Léman.
Mais le lac a une plus grande quantité de chaleur que la tasse de café, même en hiver!
•
•

La thermodynamique est la science qui s'intéresse à la chaleur et à la température, 2 grandeurs physiques très importantes. Certains de ses principes et de ses concepts comme l'entropie ont même des implications philosophiques indispensables à la compréhension de l'état du Monde et de son évolution.

Température et chaleur

Dilatation des solides

Dilatation des liquides
Cette agitation correspond à l'énergie cinétique moyenne des atomes. Plus les atomes vont vite (plus l'énergie cinétique est grande) et plus les chocs entre-eux sont violents et fréquents: on observe alors sur notre thermomètre une élévation de la température.
La chaleur est l'une des formes que peut prendre l'énergie: c'est l'énergie calorifique.

Dilatation des gaz

Loi des gaz parfaits

Théorie cinétique des gaz

Température absolue

Chaleur et énergie

= chaleur massique
Capacité thermique massique

Echange thermique et isolation

Echange d’énergie entre 2 corps



Equivalence chaleur_énergie mécanique
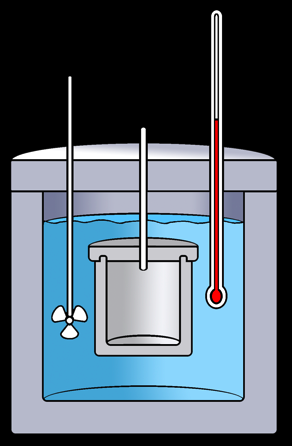
Le calorimètre
Changements d’état

2e principe de la thermodynamique




Fin de la page

Dilatation volumique
Dilatation des gaz (thermomètre à gaz , convection)

Changements d’état
3 états de la matière : solide _ liquide _ gaz
Température de fusion et d’ébullition (valeurs fixes pour un corps pur)
Chaleur latente de fusion f : Q = f . m
Chaleur latente de vaporisation v : Q = v . m
foehn ∆T = 0,5°C (montée) et 1°C à la descente (pour 100 m de dénivellation)
température de fusion dépend de la pression : glace et fil , patineur
Bouiilant de Franklin
pression de saturation (augmente avec la température)
Psat < ou = Patm 12qw
marmite à vapeur
ébullition et évaporation
hygrométrie
isotherme_isobare
Frigo
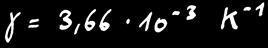

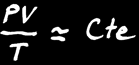

Définition:
Calculer la différence de hauteur de la Tour Eiffel entre l’hiver (0°C) et l’été (30°C) sachant qu’elle est en acier et qu’elle mesure 300m.
Que se passe-t-il dans le métal lorsqu’une partie de la tour est exposée au soleil tandis qu’une autre est à l’ombre?
Nous avons déjà vu que derrière toutes les transformations, tous les événements, il y a «quelque chose», une grandeur qui persiste: l'énergie. L'énergie peut exister sous différentes formes:
Lorsqu’on chauffe un solide de volume V1, il va se dilater et mesurera finalement le volume V2.
L’accroissement de volume (∆V) dépend de la différence de température de la barre (∆T) et de la matière étudiée.






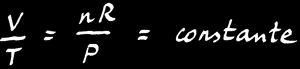
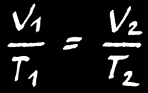


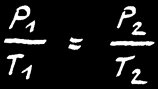



A 0°C, γ = 3,66 .10-3 K-1
On retrouve la même formule :


Dans un gaz, PV est proportionnel à T. On note:
Ce qui veut dire qu’une augmentation de température provoque soit:
une augmentation de volume
une augmentation de pression ... ou les deux !
•
•
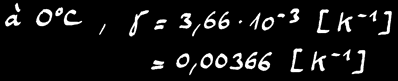
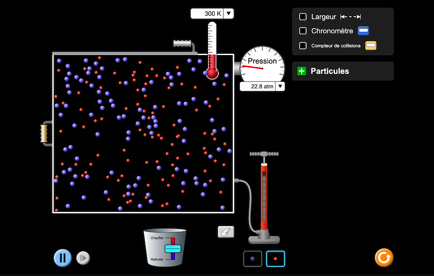
Contrairement aux solides et aux liquides, un gaz occupe tout l’espace disponible. Il y a une relation simple qui lie le volume (V), la pression (P) et la température (T) d’un gaz:


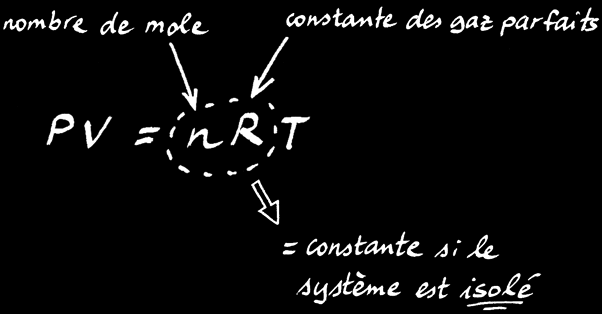
On peut transformer la relation de proportionnalité en une égalité en rajoutant 2 termes à l’équation: n et R.
On trouve alors la loi des gaz parfaits:
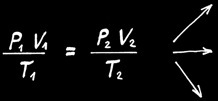
La loi des gaz parfaits est une relation simple qui lie le volume (V), la pression (P) et la température (T) d’un gaz:

Elle n’est rigoureusement juste qu’à certaines conditions:
le système doit être isolé: s’il y a un transfert de matière, le nombre de mole «n» n’est plus constant.
Le «volume propre» des molécules doit être négligeable par rapport au volume occupé par le gaz.
Les molécules ne doivent pas interagir les unes avec les autres autrement que par des chocs aléatoires.
•
•
•
Ces conditions sont réalisées chez les gaz rares: Ils sont monoatomiques et leurs atomes n’ont aucune affinité les uns pour les autres. On les trouve dans la 8e colonne du tableau périodique.
Pour tous les autres gaz, on se contentera d’une bonne approximation.

Gaz rares

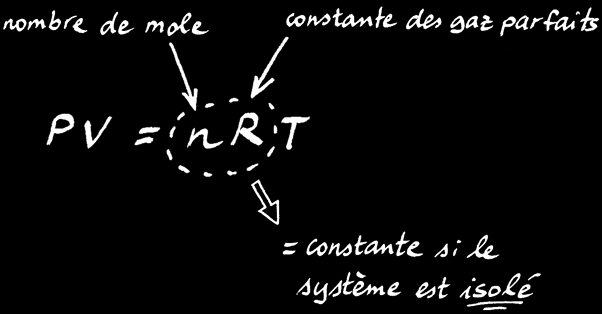
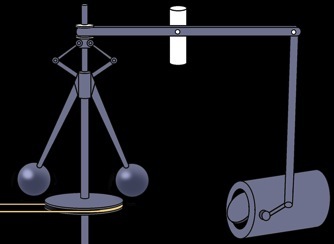
Si la réaction se fait à température constante , alors:

Si la réaction se fait à pression constante , alors:




Si la réaction se fait à volume constant , alors:




Pour la majorité des gens "c'est la même chose". Ce n'est pas vrai. Essayons d'y voir un peu plus clair.
La température est une grandeur physique mesurée à l’aide d’un thermomètre qui mesure l'agitation des atomes invisibles de la matière.

Dilatation -> densité baisse -> mouvement de convection (soupe, bain, courant marin)
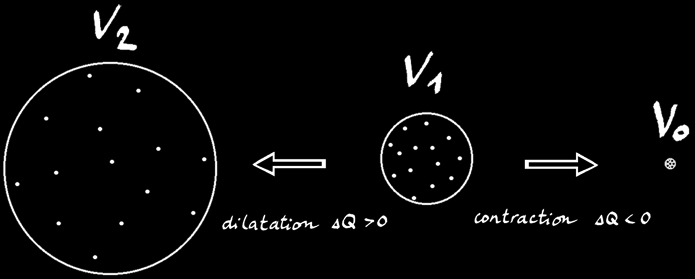
Lorsqu’un gaz de volume V1 reçoit de la chaleur (∆Q > 0) il se dilate jusqu’au volume V2. On peut noter:
V2 = V1 + ∆V
Si on refroidit le système (∆Q < 0), l’agitation du gaz diminue et son volume aussi. Dans le cas d’un gaz parfait on considère que le volume des molécules est ridiculement petit par rapport au volume occupé par les molécules.
Si nous refroidissons encore ce gaz, il arrive un moment où le mouvement des molécules de gaz devient nul: les molécules sont immobiles et n’occupent plus d’espace (avec la vision simplifiée des gaz parfaits.
On pose alors:

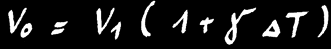


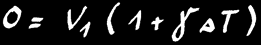

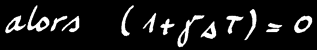

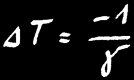
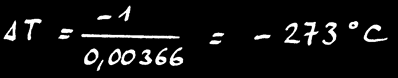



Retour au portail du corps humain




Retour au portail de physique


Retour au cours de géologie


Retour au cours d’astronomie
Retour au portail des sciences




Retour au cours de chimie












lac Léman

h
Joseph Fourier 1768-1830) étudie la propagation de la chaleur dans une barre métallique reliant une source chaude à une source froide.

Il définit le gradient thermique comme la variation de température sur une certaine longueur: ∆T/∆x
La conduction thermique, c'est à dire la quantité de chaleur qui s'écoule dans la barre pendant un certain temps est donnée par la formule:
Q = chaleur
t= temps
x = longueur
T = température
S= surface (section de la barre)
lambda = coefficient de propagation = conductivité thermique
lambda grand -> bon conducteur thermique (fer, argent, les métaux)
lambda petit -> isolant thermique = mauvais conducteur (bois, eau)
Avec:
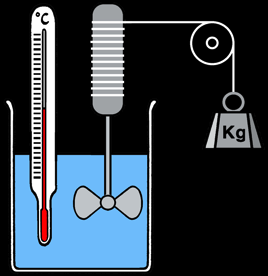
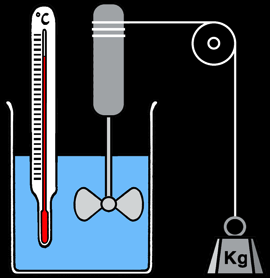
Expériences de Joule (1838-1848)
Travail fourni / chaleur produite = constante --> W/Q= J = env 4,2 Joule/Calorie
calorie _ Joule
1 cal = 4,19 J et 1J = 1N . 1m

1er principe de la thermodynamique

On se rappelle que la pression à une force qui s'exerce sur une surface....Soit un gaz enfermé dans un cylindre muni d'un piston. Chauffons ce système:
dessin .....
Le gaz se dilate, exerce une force sur le piston
F = P . S
Le travail ainsi réalisé s'écrit: ∆W = F . ∆h = P . S . ∆h = P. ∆V
La chaleur (∆Q) communiquée à un gaz permet à ce gaz:
- de fournir un travail (∆A) à l'extérieur, en repoussant un piston par exemple.
-d'accroître l'agitation ou l'énergie cinétique de ses molécules
Dans un processus adiabatique (sans échange de chaleur entre l'intérieur et l'extérieur du système) : ∆Q = 0
Gaz parfait: U proportionnel à T (pas d'énergie potentielle Ep)
Gaz "réel" : non
Sadi Carnot
Gouverne l'évolution des systèmes. Condition de transformation de la chaleur en travail: irréversibilité.
Reprenons le premier principe : ∆Q = ∆U + ∆A ou ∆Q = ∆U + ∆W
Une machine thermique (moteur) effectue des cycles. On peut donc poser ∆U=0, donc : ∆Q = ∆W
L'idée est de transformer intégralement la chaleur (∆Q) en travail mécanique(∆W).
∆Q = ∆Qc - ∆Qf = ∆W
∆Qc = ∆W + ∆Qf
Il faut donc que ∆Qf soit le plus petit possible... mais il ne peut pas être nul (le zéro absolu est un objectif impossible à atteindre!)
Il est impossible de réaliser un processus cyclique fournissant du travail à partir d'une seuler source de chaleur.
Un système évolue spontanément dans le sens d'une augmentation d'entropie
Le rendement maximum d'une machine thermique: êta max = 1 - Tf/Tc
êta = ∆W/∆Qc
Le premier principe de la thermodynamique est un principe d'équivalence_Rudolf Clausius, vers 1850
∆Q = ∆U + ∆A
avec:
Q = chaleur
U = énergie interne (énergie totale à l'intérieur du système)
A = travail (de l'allemand "Arbeit" ) .... ou ∆W (de l'anglais "Work" )




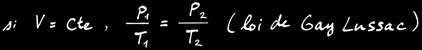



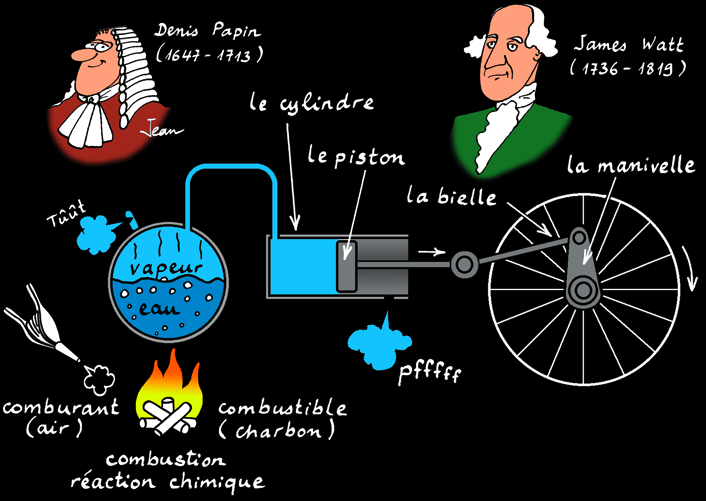
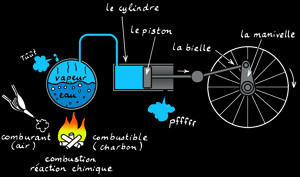

La machine à vapeur
La machine à vapeur est un moteur à combustion externe: la réaction a lieu à l'extérieur du cylindre. L'énergie thermique produite par la réaction de combustion est transmise à une chaudière qui contient de l'eau. Arrivée à la température d'ébullition, l'eau passe de l'état liquide à l'état gazeux (vapeur). Cette vapeur occupe un plus grand volume et exerce une pression dans la chaudière. La vapeur est canalisée dans un tuyau jusqu'à une chambre (le cylindre) dont une des parois est mobile: le piston). Le piston se déplace en coulissant dans le cylindre: on a transformé l'énergie thermique en énergie mécanique: un mouvement linéaire.
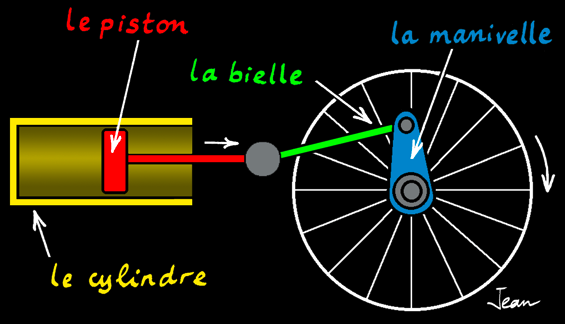
Le système bielle-manivelle est un système mécanique qui transforme un mouvement linéaire alternatif en un mouvement de rotation.
Avantage: on peut utiliser n'importe quel combustible (charbon, bois, pétrole ,..) et faire tourner des machines en absence de vent (moulin à vent) et loin des rivières (moulin à eau).
Inconvénient: il faut attendre que la chaudière produise de la vapeur et les pertes de chaleur sont énormes.
perfectionnements de Watt entre 1760 et 1790
La double action permet un gain de puissance...
Le régulateur à boules est un système qui permet de régler la vitesse de rotation de la machine à vapeur.


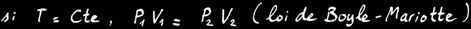



Animation «gaz»

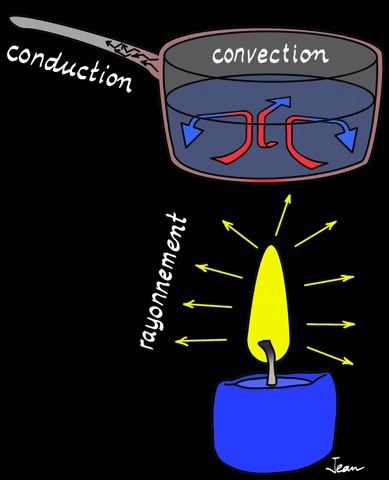
Lorsqu’on chauffe un solide , ses atomes s’agitent dans tous les sens et s’entrechoquent. Ces chocs se propagent de plus en plus loin: c’est ainsi que l’extrémité du manche de la casserole finit par recevoir la chaleur produite par la flamme.
Lorsqu’on chauffe un fluide (liquide ou gaz), les atomes ou les molécules qui le constituent s’agitent: le fluide se dilate, devient moins dense (plus «léger») et s’élève. Lorsqu’il se refroidit il se contracte, devient plus dense («plus lourd») et redescend.
La matière chaude émet un rayonnement qui se propage dans l’espace et même dans le vide. C’est ainsi que le soleil peut nous chauffer alors qu’il se trouve à une distance de 150 millions de kilomètres. Ce rayonnement de chaleur s’appelle infra-rouge (IR) et fait partie de la famille des rayons électromagnétiques comme la lumière:
La chaleur (énergie calorifique) peut migrer dans l’espace suivant 3 «moyens de transport» : la convection, la conduction et le rayonnement.

La convection


Le rayonnement
La conduction

Transmission de la chaleur